【Python, Google Drive】体重管理&解析アプリを作ろう6 ~回帰分析1~

体重トレンド解析を実装する自分だけのWebアプリを作成するため、前回記事までに登録フォーマットの原型を作成し、データの特徴量を算出した後にデータをグラフ化しました。

2022.02.20

今回は、統計学の単解析分析を用いて、体重及び体脂肪量の予測を行います。単回帰分析がよくわからない方は以下のサイトがわかりやすいと思います。

【Pythonで学ぶ】回帰分析を図でわかりやすく解説！条件付き平均と最小二乗法って？【データサイエンス入門:統計編13】

27-1. 単回帰分析
27-1. 単回帰分析

それでは単回帰分析を実施するコードを記載していきます。

▼ Contents

1. 使用するデータテーブル

今回使用するデータはTable1に示す体重と体脂肪率です。

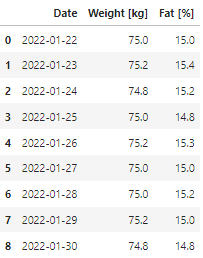
前回までの記事をご参考いただきご自身のデータを作成いただくか、以下のコードでサンプルデータフレームを用意することが可能です。

dct = {
    'Date': ["2022-1-22", "2022-1-23", "2022-1-24", "2022-1-25", "2022-1-26", "2022-1-27", "2022-1-28", "2022-1-29", "2022-1-30"],
    'Weight [kg]': [75.0, 75.2, 74.8, 75.0, 75.2, 75.0, 75.0, 75.2, 74.8],
    'Fat [%]': [15.0, 15.4, 15.2, 14.8, 15.3, 15.0, 15.2, 15.0, 14.8]
    }
df = pd.DataFrame(dct)
df

データが準備できましたら、単回帰分析を行っていきましょう。

2. 単回帰分析

ここから単回帰分析を行います。まずは使用するライブラリをインポートしておきましょう。

import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression

次に目的関数(ターゲット)を指定します。ここでは”体重(Weight [kg])”を指定します。

また、目標体重(target_weight)と予測したい日にち(predict_day)を指定します。今回は目標70kgと30日後を予測したいとします。

target = 'Weight [kg]'
target_weight = 70
predict_day = 30

次に分析結果を格納するための辞書型格納先を準備します。

reg_sum = {}

続いて、単回帰分析するためのデータを用意します。Xは説明変数で経過日数とし初期値を0とします。サンプルデータでは2022-1-22が初期値つまり経過日数0となります。yは目的関数で予測したデータを指定します。ここでは体重となります。

なお、Xは分析する際にデータを2次元配列を変更する必要があるため、reshape関数で2次元配列にしています。

X, y = np.arange(len(df)).reshape(-1, 1), df[target]
X, y

実行すると、以下のようなデータ配列が出力されます。

(
    array([[0], [1],[2],[3],[4],[5],[6],[7],[8]]),
    array([75. , 75.2, 74.8, 75. , 75.2, 75. , 75. , 75.2, 74.8])
)

データが準備できましたら、以下のコードで単回帰分析を実行します。

reg = LinearRegression().fit(X, y)

実行できたましたら、以下のコードで辞書型格納先のreg_sumに値を格納していきます。

Feature: ターゲット名
Coef: 単回帰分析の傾き、予測に使用する
Intercept: 単回帰分析の切片、今回の解析では未使用
Predict: 単回帰分析の傾きから予測日のターゲット値、今回は30日後を予測

reg_sum['Features'] = target
reg_sum['Coef'] = round(reg.coef_[0], 4)
reg_sum['Intercept'] = round(reg.intercept_, 1)
reg_sum[f'Predict ({predict_day}days)'] = reg.predict([[len(df)+predict_day]]).round(1)

最後に目標体重(target_weight)と予測したい日にち(predict_day) から、目標体重に到達する日数と、predict_day日後の体重の予測結果を表示するコードを記載します。

target_date_weight = (target_weight - df['Weight [kg]'].iloc[-1]) // reg_lst[0]["Coef"]
print(f'体重{target_weight}[kg]まで{target_date_weight}日です')
print(f'{day}日後には、体重は{reg_lst[0][f"Predict ({day}days)"]}[kg]と予測されます')

実行すると、以下のような結果が出力されます。

体重70[kg]まで716.0日です
30日後には、体重は74.8[kg]と予測されます

体重70kgまではかなり長い道のりですね。。。

こちらで基本的な単回帰分析は以上です。次は複数の目的関数に対応できる単回帰分析の関数を作成します。

3. 複数の単回帰分析を実行する

前章のコードを参考に複数の目的関数を単回帰分析関数を作成しましょう。といってもfor文で目的関数ごとに単回帰分析を行うのみなのでかんたんです。

まずは、各分析結果を格納するリストを用意します。

reg_lst = []

次にターゲットとなる目的関数のカラム名をリスト型としてまとめておきます。また、目標体重(target_weight)と目標体脂肪量(target_fat)および予測したい日にち(predict_day)を指定します。今回は目標70kg, 12%と30日後を予測したいとします。

targets = ['Weight [kg]', 'Fat [%]']
target_weight, target_fat = 70, 12
predict_day = 30

あとは目的関数ごとにfor文で前章と同じ分析を繰り返します。

for target in targets:
    reg_sum = {}
    X, y = np.arange(len(df)).reshape(-1, 1), df[target]
    reg = LinearRegression().fit(X, y)
    reg_sum['Features'] = target
    reg_sum['Coef'] = round(reg.coef_[0], 4)
    reg_sum['Intercept'] = round(reg.intercept_, 1)
    reg_sum[f'Predict ({day}days)'] = reg.predict([[len(df)+predict_day]])[0].round(1)
    reg_lst.append(reg_sum)
reg_lst

実行すると以下のような、リスト型の結果を得ることができます。

[
 {'Features': 'Weight [kg]', 'Coef': -0.0067, 'Intercept': 75.0, 'Predict (30days)': 74.8},
 {'Features': 'Fat [%]', 'Coef': -0.03, 'Intercept': 15.2, 'Predict (30days)': 14.0}
]

最後にリスト型の結果を使用して、分析結果を計算、表示するようにします。

target_date_weight = (target_weight - df['Weight [kg]'].iloc[-1]) // reg_lst[0]["Coef"]
target_date_fat = (target_fat - df['Fat [%]'].iloc[-1]) // reg_lst[3]["Coef"]
print(f'体重{target_weight}[kg]まで{target_date_weight}日です')
print(f'体脂肪率{target_fat}[%]まで{target_date_fat}日です')
print(f'{predict_day}日後には、体重は{reg_lst[0][f"Predict ({day}days)"]}[kg]と予測されます')
print(f'{predict_day}日後には、体脂肪率は{reg_lst[3][f"Predict ({day}days)"]}[%]と予測されます')

以上で単回帰分析は終了です。他の目的関数も同様に分析できるので試してみてください。

4. まとめコード

今回の分析コードを”single_reg”関数としてまとめています。次回は重回帰分析を取り入れてみます。

import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression

def single_reg(df, target_weight, target_fat, day=30):
    targets = ['Weight [kg]', 'Fat [%]']
    reg_lst = []
    for target in targets:
        reg_sum = {}
        X, y = np.arange(len(df)).reshape(-1, 1), df[target]
        reg = LinearRegression().fit(X, y)
        reg_sum['Features'] = target
        reg_sum['Coef'] = round(reg.coef_[0], 4)
        reg_sum['Intercept'] = round(reg.intercept_, 1)
        reg_sum[f'Predict ({day}days)'] = reg.predict([[len(df)+day]])[0].round(1)
        reg_lst.append(reg_sum)
    target_date_weight = (target_weight - df['Weight [kg]'].iloc[-1]) // reg_lst[0]["Coef"]
    target_date_fat = (target_fat - df['Fat [%]'].iloc[-1]) // reg_lst[3]["Coef"]
    print(f'体重{target_weight}[kg]まで{target_date_weight}日です')
    print(f'体脂肪率{target_fat}[%]まで{target_date_fat}日です')
    print(f'{day}日後には、体重は{reg_lst[0][f"Predict ({day}days)"]}[kg]と予測されます')
    print(f'{day}日後には、体脂肪率は{reg_lst[3][f"Predict ({day}days)"]}[%]と予測されます')

single_reg(df, target_weight=70, target_fat=12, day=30)

以下は本記事の関連記事となります。随時更新中ですので公開次第、リンクを貼り付けていきます。