Dockerで環境構築、jupyterlabおよびPythonを使用して、Twitter機能の一つであるTwitterアナリティクスのデータを分析しています。今回は、忘備録を兼ねて、t値の意味とpython sk-learnでの算出方法をまとめておきます。本記事を読むと、
- Twitterデータで重回帰分析(sk-learn)におけるt値の概要がわかる
- 分析用のサンプルコード(Python)を使用できる
ので、ぜひ最後までご覧いただけると幸いです。
なお、サンプルコードは最後に記載していますので、サンプルコードだけほしい方は、目次リンクで飛んでいただけると幸いです。それではやっていましょう!
▼ Contents
1. t値やp値とは何か
そもそも、t値や関連するp値ってなに?がわからなかったので、ググってみたところ、
回帰分析におけるt検定の具体的な方法は、
説明変数の係数が本当はゼロであるという仮説(帰無仮説)を立て、検定統計量“t値”を計算し、有意水準を決め、その有意水準に対応するt値の臨界値と2で求めた検定統計t値を比較する。検定統計量t値の絶対値が臨界値の絶対値より小さい場合には、帰無仮説を正しいとして採択するが、そうでなくt値の絶対値が臨界値の絶対値より大きくなった場合には、帰無仮説を誤りとして捨て去り(棄却)、それとは反対の「係数がゼロとはいえない」という仮説(対立仮説)を採択する。
回帰分析におけるt値とp値の意味について(抜粋)
重回帰分析の結果はαを切片、βを各説明変数の係数、xi(i = 1, 2, …n)をn個の説明変数とすると、以下の式で目的変数y_nが算出される。
$$y_n=\alpha + \beta_1x_1+\beta_2x_2+…+\beta_ix_i+…+\beta_nx_n (i = 1, 2, …n)$$
どうやら、回帰分析におけるt検定とは、βiが特定の値β0(多くの場合は0とする)と比較して、βがその特定の値になるかどうかを検討しているようです。
なぜ、特定の値β0を0とするかというと、βiが0の場合、説明変数xiがいかなる値でも、βiとxiの乗算は0となるため、目的変数ynに影響しないためです。
そのため、回帰分析におけるt検定とは、
帰無仮説:各説明変数の係数βiが0である
対立仮説:各説明変数の係数βiが0ではない
として、帰無仮説が起こる確率が有意水準(一般的には5%)を超える場合、帰無仮説を採用し、有意水準を超えない場合は対立仮説を採用する。
つまり、有意水準を超えた説明変数は各説明変数の係数βiが0である確率が高いため、棄却しても統計学的に影響は少ないということだそうです。
ちなみにp値は、t値が起こる累積確率を表しているようです。
P値とはどんな意味?
有意水準を5%とした場合、(t値の絶対値)>=2もしくはp値<=0.05であれば、帰無仮説の条件が起こる確率が低いため、帰無仮説を棄却して対立仮説を採用するようです。
2. pythonでのt値算出
t値の算出方法は以下を参考にしました。
回帰分析のt値の求め方
回帰分析のt値の求め方:Pythonで実装
def std_err(self, reg, x, y):
y_hat = reg.predict(x)
n = x.shape[0]
p = x.shape[1]
sse = np.sum((y - y_hat) **2, axis=0)
sse = sse / (n - p -1)
s = np.linalg.pinv(np.dot(x.T, x))
std_err = np.sqrt(np.diagonal(sse * s))
return std_err
a = reg.coef_.round(4)
t_values = (a / self.std_err(reg, x, y))以上のコードを前回のコードに組み込んでおきます。コード詳細はこちらをご覧いただけると幸いです。
3. サンプルコードとまとめ
ファイルフォルダー構成は以下です。
.
|-- Twitter_analytics.ipynb
|-- data
| `-- tweet_activity_metrics_BaranGizagiza_YYYYMMDD_YYYYMMDD_ja.csv
|-- data_base_analytics.py
`-- evaluation_analytics.py各ファイルは以下となります。
""" Twitter_analytics.ipynb """
import base_analytics as ba
import evaluation_analytics as ea
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.feature_selection import f_regression
"""1.準備編 """
ba_Inst = ba.Data_path()
twitter_data_path = ba_Inst.data_path()
twitter_df = ba_Inst.data_df(twitter_data_path)
twitter_df = ba_Inst.data_en(twitter_df)
twitter_df = ba_Inst.data_time(twitter_df)
""" 5.Tweet分析編 """
string_list = ['Python', '読書', 'ブログ', '筋トレ', '統計', 'エンジニア', 'datascientist']
ea_Inst = ea.Eva_Inst()
ea_Inst.evaluation_string(twitter_df, string_list)""" 7.重回帰分析編(その1) """
string_list = ['Impression', 'RT', 'Return', 'Python', \
'読書', 'ブログ', '筋トレ', '統計', 'エンジニア', 'datascientist']
def std_err(self, reg, x, y):
y_hat = reg.predict(x)
n = x.shape[0]
p = x.shape[1]
sse = np.sum((y - y_hat) **2, axis=0)
sse = sse / (n - p -1)
s = np.linalg.pinv(np.dot(x.T, x))
std_err = np.sqrt(np.diagonal(sse * s))
return std_err
x2 = twitter_df[string_list]
y2 = twitter_df['Good']
reg = LinearRegression()
results = reg.fit(x2,y2)
r2 = reg.score(x2,y2).round(4)
n = x2.shape[0]
p = x2.shape[1]
adjusted_r2 = (1-(1-r2)*(n-1)/(n-p-1)).round(4)
a2 = reg.coef_.round(4)
t_values = (a2 / self.std_err(reg, x2, y2)).round(4)
f_values = f_regression(x2,y2)[0].round(4)
p_values = f_regression(x2,y2)[1].round(4)
reg_summary = pd.DataFrame(data = x2.columns.values, columns=['Features'])
reg_summary ['Coefficients'] = a2
reg_summary ['t-values'], reg_summary ['f-values'], reg_summary ['p-values'] =\
t_values, f_values, p_values
new_data = pd.DataFrame(data=[[2000, 1, 0, 1, 1, 1, 1, 1, 1, 0]],columns=string_list)
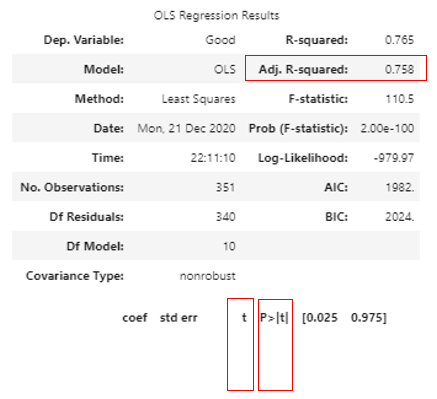
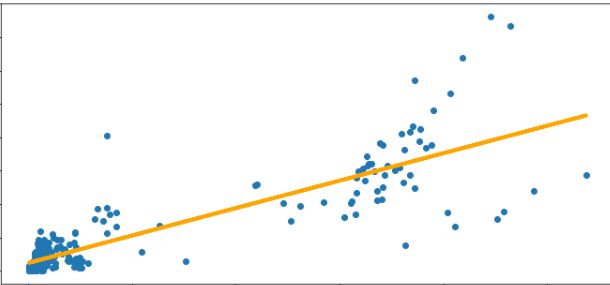
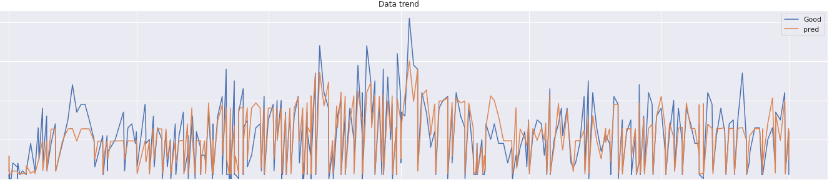
reg.predict(new_data).round(4)t値やp値が定めた有意水準を超えている場合、その変数は’Good’数を予測する上で、統計学上では棄却しても問題ないということでした。
それでは、よいPythonライフを!!

本記事に関連する過去の投稿は以下です。ご覧いただけると幸いです。





コメントを残す